排序的升级版—快速排序以及归并排序

一，归并排序（英语：Merge sort，或mergesort）。

1，排序思想：

是创建在归并操作上的一种有效的排序算法，效率为O(n log n)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。归并排序的核心思想是将两个有序的数列合并成一个大的有序的序列。通过递归，层层合并，即为归并。

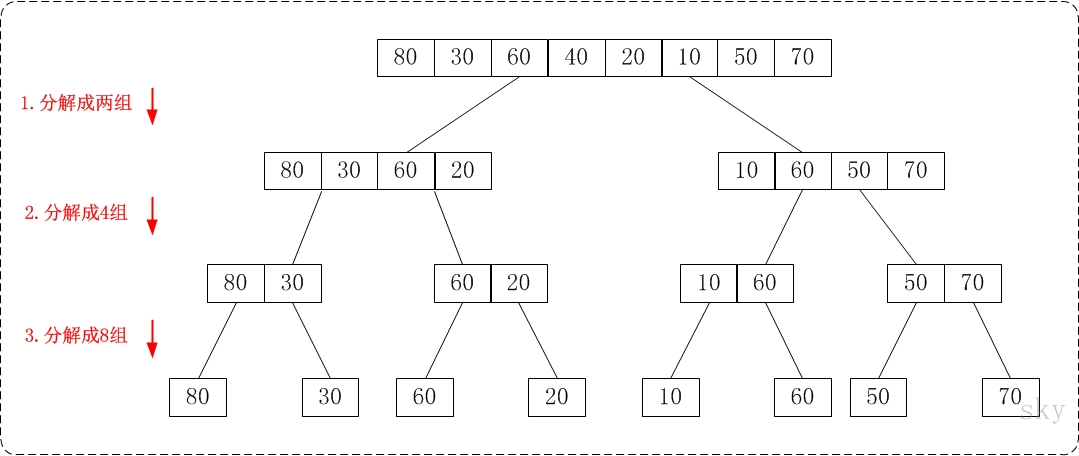
2，开始代码

    1），传入一个数组以及数组的长度

/**
 * 归并排序 nlogn
 * @param arr
 * @param length
 */
public static void mergeSort(int[] arr,int length){
    __mergeSort(arr,0,length - 1);
}

    2），对数组的 arr[l,r]范围进行排序，l为左边界，r为右边界，注意是左闭右闭的区间。

/**
 * 对arr[l,r]范围进行排序
 * @param arr
 * @param l
 * @param r
 */
public static void __mergeSort(int[] arr,int l,int r){
    if(l >= r){        // 跳出递归的条件
        return;
    }
    int mid = (l + r)/2;        //计算中点位置
    __mergeSort(arr,l,mid);        // 调用自身对左部分区间进行排序
    __mergeSort(arr,mid + 1,r);    // 调用自身对右部分区间进行排序
    if(arr[mid] > arr[mid + 1]){      //如果是近乎有序的数组，可以这样优化
        __merge(arr,l,mid,r);        // 开始归并并排序
    }
}

    3），对arr[l,mid] 和  arr[mid +1 ,r] 两部分进行归并

    /**    
     * 对arr[l,mid] 和  arr[mid +1 ,r] 两部分进行归并
     * @param arr
     * @param l
     * @param mid
     * @param r
     */
    public static void __merge(int[] arr,int l,int mid,int r){
    	int[] aux = new int[r - l + 1];
    	for(int i = l;i <= r;i++){
    		aux[i - l] = arr[i];
    	}
    	
    	int i = l;
    	int j = mid + 1;
    	for(int k = l;k <= r;k++){
    		if(i > mid){
    			arr[k] = aux[j - l];
    			j++;
    		}else if(j > r){
    			arr[k] = aux[i - l];
    			i++;
    		}else{
    			if(aux[i - l] < aux[j - l]){
    				arr[k] = aux[i -l];
    				i++;
    			}else{
    				arr[k] = aux[j -l];
    				j++;
    			}
    		}
    		
    	}
    }

以上就是归并排序，优化的话，可以在数组小于一定容量时，改为插入排序，增加效率。

if(l >= r){
     return;                             // 跳出递归的条件
 }
 // 我们可以改成以下
 if(r - l < 15){
     insertSort(arr,l,r);
     return;
 }

附上插入排序的代码：

    /**    
     *    插入排序，对[l,r]区间的arr数组插入排序
     */
    public static void insertSort(int[] arr,int l,int r){
		for(int i = l + 1; i <= r; i++){
			int e = arr[i];
			int j;
			for(j = i;j > l && arr[j - 1] > e;j--){
				arr[j] = arr[j - 1];
			}
			arr[j] = e;
	    }
		return;
	}

二，快速排序（英语：Quicksort）。

    1，算法思想

基于分治的思想，是冒泡排序的改进型。首先在数组中选择一个基准点（该基准点的选取可能影响快速排序的效率，后面讲解选取的方法），然后分别从数组的两端扫描数组，设两个指示标志（low指向起始位置，high指向末尾)，首先从后半部分开始，如果发现有元素比该基准点的值小，就交换low和high位置的值，然后从前半部分开始扫秒，发现有元素大于基准点的值，就交换low和high位置的值，如此往复循环，直到low>=high,然后把基准点的值放到high这个位置。一次排序就完成了。以后采用递归的方式分别对前半部分和后半部分排序，当前半部分和后半部分均有序时该数组就自然有序了。

    2，开始代码

        1），同样传入一个数组，和数组的长度。

/**
 * 快速排序
 * @param arr
 * @param length
 */
public static void quickSort(int[] arr,int length){
    __quickSort(arr,0,length - 1);
}

        2），对arr[l,r]部分进行快速排序。

/**
 * 对arr[l,r]部分进行快速排序
 * @param arr
 * @param l
 * @param r
 */
public static void __quickSort(int[] arr,int l,int r){
    if(l >= r){
        return;
    }
    int p = __partition2(arr,l,r);
    __quickSort(arr,l,p-1);
    __quickSort(arr,p+1,r);
}

        3），对arr[l,r]部分进行partition操作，返回p，使得arr[l,p-1] < arr[p], arr[p+1] > arr[p]

/**
 * 对arr[l,r]部分进行partition操作，返回p，使得arr[l,p-1] < arr[p], arr[p+1] > arr[p]
 * @param arr
 * @param l
 * @param r
 * @return
 */
public static int __partition(int[] arr,int l,int r){
    int temp1 = arr[l];
    arr[l] = arr[new Random().nextInt(r - l + 1) + l];
    arr[new Random().nextInt(r - l + 1) + l] = temp1;

    int v = arr[l];
    int j = l;
    for(int i = l + 1;i <= r; i++){
        if(arr[i] < v){
            int temp = arr[j + 1];
            arr[j + 1] = arr[i];
            arr[i] = temp;
            j++;
        }
    }
    int temp = arr[j];
    arr[j] = arr[l];
    arr[l] = temp;
    return j;
}

改进版本，双路同时进行。

/**
 * 改进版
 * @param arr
 * @param l
 * @param r
 * @return
 */
public static int __partition2(int[] arr,int l,int r){
    int temp1 = arr[l];
    int index = new Random().nextInt(r - l + 1) + l;
    arr[l] = arr[index];
    arr[index] = temp1;

    int v = arr[l];
    int i = l + 1;
    int j = r;
    while(true){
        while(i <= r && arr[i] < v){
            i ++;
        }
        while(j >= l + 1 && arr[j] > v){
            j --;
        }
        if(i > j){
            break;
        }
        int temp2 = arr[j];
        arr[j] = arr[i];
        arr[i] = temp2;
        i++;
        j--;
    }
    int temp3 = arr[j];
    arr[j] = arr[l];
    arr[l] = temp3;
    return j;
}

快速排序的终极版本，三路快速排序。

/**
 * 三路快速排序
 * @param arr
 * @return
 */
public static void threeWaysQuickSort(int[] arr,int length) {
    __threeWaysQuickSort(arr,0,length - 1);
}

public static void __threeWaysQuickSort(int[] arr,int l,int r) {
    if(r - l < 15){
        insertSort(arr, r,l);
    }

    int index = new Random().nextInt(r - l + 1) + l;
    int temp1 = arr[l];
    arr[l] = arr[index];
    arr[index] = temp1;

    int v = arr[l];
    int lt = l;
    int gt = r + 1;
    int i = l + 1;
    while(i < gt){
        if(arr[i] < v){
            int temp2 = arr[lt + 1];
            arr[lt + 1] = arr[i];
            arr[i] = temp2;
            lt++;
            i++;
        }else if(arr[i] < v){
            int temp3 = arr[gt - 1];
            arr[gt - 1] = arr[i];
            arr[i] = temp3;
            gt--;     // 这里没有 i++操作，因为交换来的值仍旧需要考察
        }else{
            i++;
        }
    }
    int temp4 = arr[lt];
    arr[lt] = arr[l];
    arr[l] = temp4;

    __threeWaysQuickSort(arr, l, lt - 1);  // 减一是因为arr[l] 与 arr[lt] 交换了，lt-1才是不包含v的范围
    __threeWaysQuickSort(arr, gt, r);
}

以上就是对归并以及快速排序的总结，理解有点难度，需要花点时间。